I- Résistances en série:
On mesure à l’ohmmètre nos résistances :
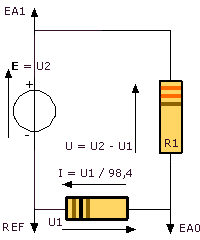
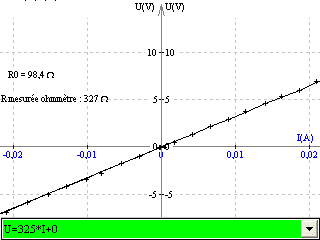
R1 = 97 W (M.N.M)
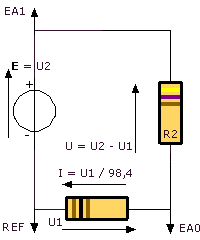
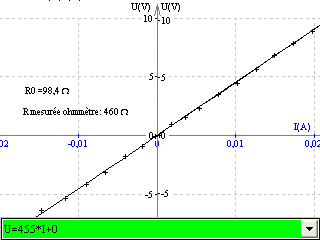
R2 = 325 W (O.O.M)
R3 = 460 W (J.Vi.M)
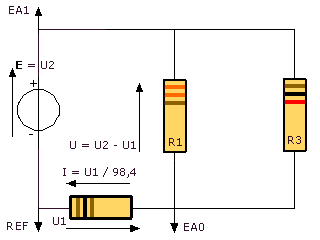
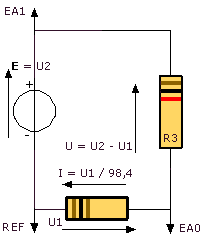
1°) Montage expérimental: (EXAO)
AB est le dipôle à l’étude

On peut ainsi considérer que RAB = R2 + R3 et
généraliser pour n résistances R1, R2, ..., Rn en série:
Réq = R1 + R2 + ... + Rn
3°) Conclusion:
Lorsque des résistances sont montées en série, la résistance équivalente
de l’association est la somme de toutes les résistances.
Lorsque des résistances sont en série, la résistance totale est forcément plus grande que la plus grande des résistances.
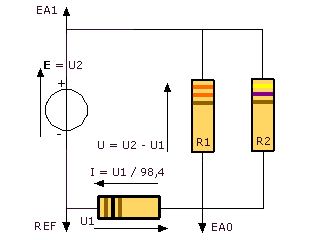
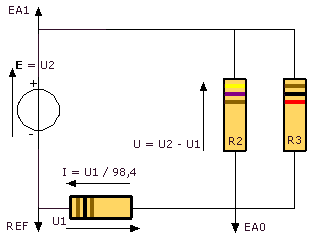
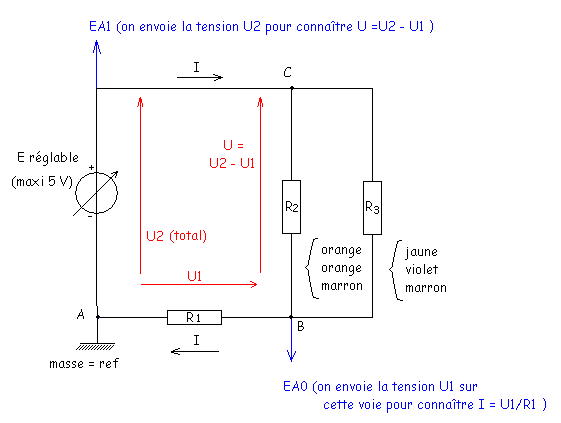
II- Résistances en dérivation: (EXAO)
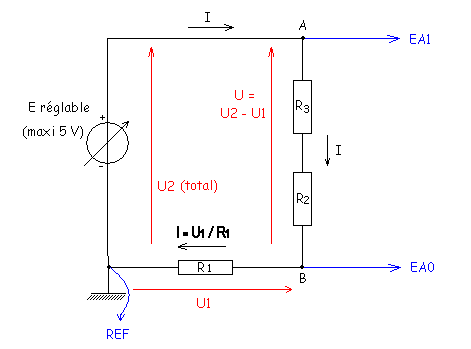
1°) Montage expérimental:
BC est le dipôle à l’étude
3°) Conclusion:
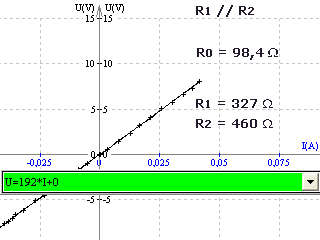
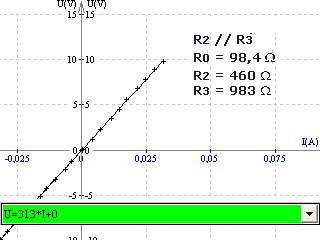
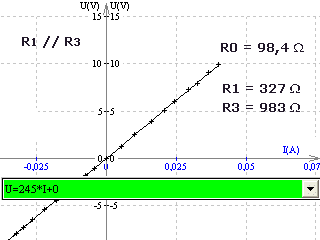
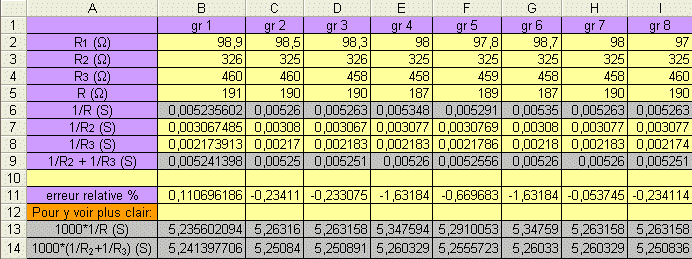
La comparaison des lignes 6 et 9 ou 13 et 14 montre que leur contenu est à peu près égal et nous admettons donc que:
1/R = 1/R2 + 1/R3
et nous généralisons en écrivant que:
1/Req = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn.
L’inverse de la résistance est la conductance G = 1 / R. L’inverse de l’ohm est le siemens (symbôle S).
On peut donc écrire:
Géq = G1 + G2 + ... + Gn pour n résistances en dérivation.
En dérivation, plus il y a de résistance, "moins c’est résistant"
(on offre en fait plus de
chemins possibles au courant et il passe mieux, la résistance équivalente est plus
petite que la plus petite des résistances individuelles).
Cas de deux résistances R1 // R2
1/Req = 1/R1 + 1/R2 = (R2 + R1) /R1 * R2 =>
Req = R1 × R2 /( R1 + R2 ) = produit / somme.
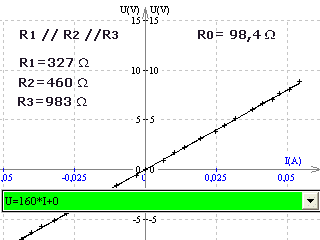
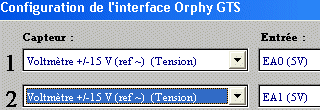
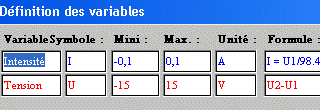
4°) Autre manipulation: tracé des 3 caractéristiques individuelles puis de celle de l'association en dérivation
Réglages de l'interface:


Résistances individuelles:



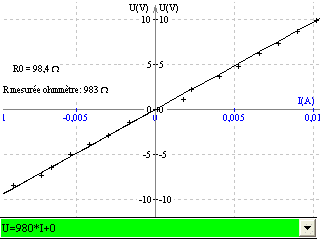
Les association en dérivation: