Le but est de savoir comment on peut remplacer deux résistances en série ou deux résistances en dérivation par une résistance unique et avoir les mêmes effets sur le reste du circuit.
On mesure à l’ohmmètre nos résistances :
R1 = 97 W (M.N.M)
R2 = 325 W (O.O.M)
R3 = 460 W (J.Vi.M)
1°) Montage expérimentale (EXAO) AB est le dipôle à l’étude 2°) Mesures (EXAO) On veut trouver la résistance équivalente à l’association en parallèle de R2 et de R3.
Il nous faut trouver une relation U = RI. 3°) Conclusion
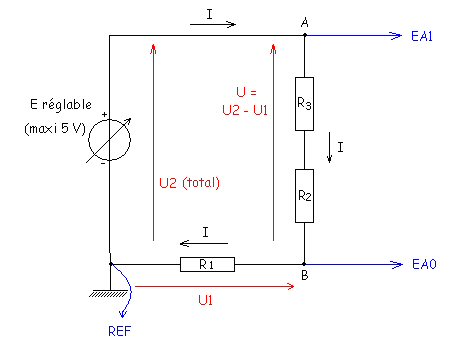
Le dipôle AB (constitué de R2 et R3 en série) suit aussi la loi d’ohm.
UAB = RAB x I avec RAB = 785 W
Or R1 + R3 = 325 + 460 = 785 W
On considère que RAB = R2 + R3
Lorsque deux résistances sont montées en série, la résistance équivalente de l’association et la somme des deux résistances.
II- Résistances en dérivation (EXAO)
1°) Montage expérimental
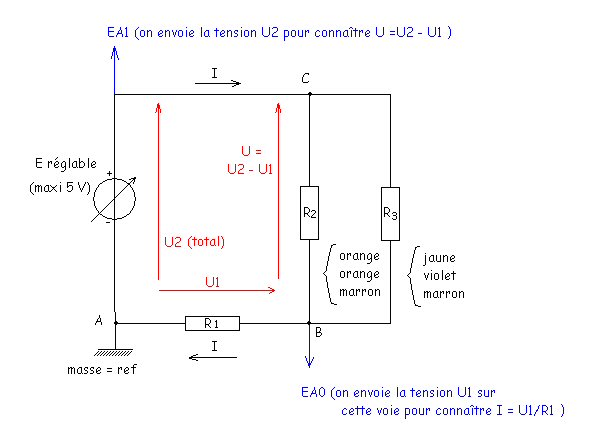
2°) Mesures et courbes
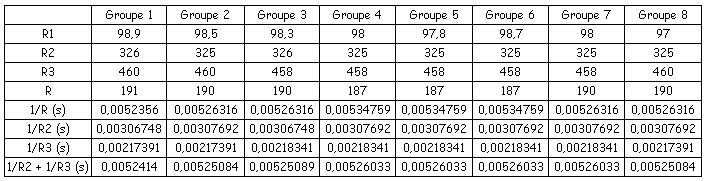
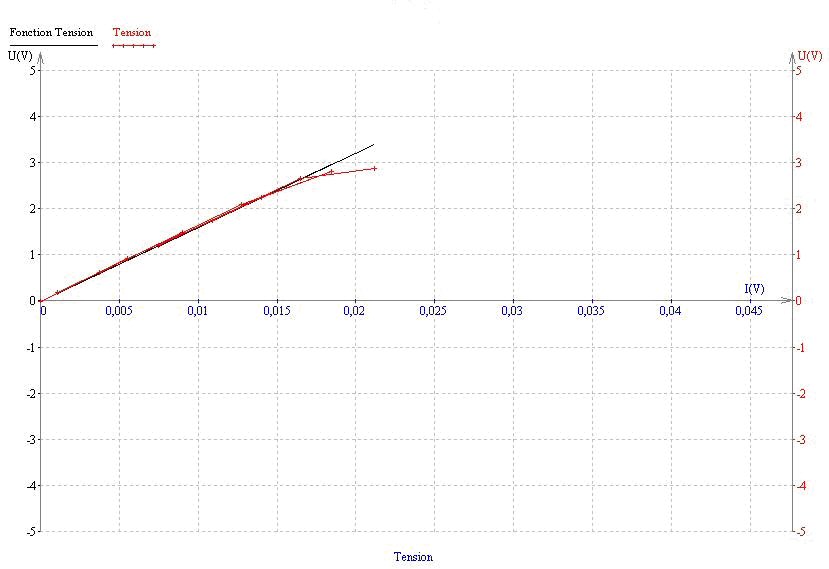
La comparaison des lignes 6 et 9 montre que leur contenu est à peu près égal et nous admettons donc que
1/R = 1/R2 + 1/R3 (ici) et nous généralisons en écrivant que 1/Req = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn.
L’inverse de l’ohm est le siemens.
Lorsqu’on a des résistances en dérivations, l’inverse de la résistance équivalente est égale à la somme des inverses
des résistances de la dérivation.
Plus on ajoute de résistance, plus c’est résistant. La résistance totale est forcément plus grande que la plus grande
des résistances.
En dérivation au contraire, plus il y a de résistance, moins c’est résistant (on offre en fait plus de chemin possible
au courant et il passe de mieux en mieux, la résistance équivalente est forcément plus petite que la plus petite des
résistances individuelles).
• Cas de deux résistances R1 // R2
1/Req = 1/R1 + 1/R2 = R2 + R1 /R1 x R2 => Req = R1 x R2 /R1 + R2 = produit/somme
La différence entre la ligne 9 et 6 nous donne l’incertitude absolue. Cet écart divisé par la ligne 6, nous donne l’erreur
relative. L’erreur absolue a une unité et l’erreur relative n’a pas d’unité et on peut l’exprimer en % si on la multiplie
par 100.
• Application : R1 // R2 // R3
1/Req = 1/R1 + 1/R2 + 1/R3