Bille glissant sur une sphère

 Soit une petite boule glissant sans rouler sur une sphère de rayon r et M₀ sa position d'équilibre instable initiale.

La liaison est parfaite; il n'y a pas pas de forces de frottement. La réaction se réduit à sa composante normale R_n.

Ecartée sans vitesse initiale de cette position, la bille se trouve en mouvement de translation circulaire dans le référentiel terrestre supposé galiléen.

Soit M la position de son centre d'inertie à l'instant générique t.

La question est:  pour quelle valeur de la bille quitte-t'elle la sphère?

 Remarque 1 : la réaction normale R_n ne travaille pas.

Remarque 2: la position d'équilibre M₀ est dite instable car si on écarte légèrement la bille de cette position, elle n'y reviendra pas.

Remarque 3: la position d'équilibre J, à l'intérieur de la sphère est dite stable car si on écarte la bille de cette position, elle y repassera et y restera, une fois son énergie dissipée complètement à cause des frottements solides et fluides.

Ecrivons la deuxième loi de Newton en un instant générique t lorsque la bille est au point générique M:

 Projetons cette relation sur le vecteur unitaire

( Note importante: ce vecteur   ne peut être attaché à un répère galiléen, puisqu'il tourne dans le référentiel terrestre: ce n'est qu'un repère de projection des lois de la Dynamique, lesquelles, elles, sont appliquées dans le référentiel terrestre supposé galiléen)

Pour que le contact demeure, il faut qu'il y ait une réaction R > 0 soit

or

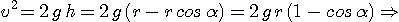
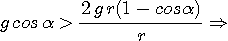
au-delà de cette valeur, la bille quitte la piste.

Le résultat ne dépend ni de la masse de la bille, ni du rayon de la sphère.