Mouvement
d'un corps dans un champ de pesanteur uniforme
A - Situation étudiée:
|

Voir
l'animation virtuelle
|
|
On lance avec une vitesse initiale  un objet non chargé de masse m constante dans une région assez
petite pour que l'intensité de la pesanteur puisse être considérée
comme constante. un objet non chargé de masse m constante dans une région assez
petite pour que l'intensité de la pesanteur puisse être considérée
comme constante.
On choisit le point O comme étant le point de départ
du mobile M.
On choisit un plan xOz contenant  et de la façon suivante: et de la façon suivante:
L'axe Ox est horizontal, dans le sens du mouvement
initial.
L'axe Oz est vertical et dirigé vers le haut.
On choisit un axe Oy perpendicualire aux 2 précédents,
donc horizontal et tel que le trièdre Ox, Oy, Oz soit direct ou
encore tel que:

On note  l'angle orienté l'angle orienté  . .
|
B - Système:
Le projectile de masse m constante, non chargé.
C - Référentiel:
Terrestre supposé galiléen.
D - Bilan des forces:
a- Poids  , vertical, dirigé vers le bas, de norme:
, vertical, dirigé vers le bas, de norme:

b - Résistance de l'air négligée ( c'est notre approximation
la moins justifiée ). Elle peut être importante; c'est en partie pour celà que
les avions volent à 30 000 pieds environ. Elle dépend de la vitesse: F = - k V
( en régime laminaire ), F = - k V2 ou F = - k V3
ou plus complexe dans les régimes turbulents. Les derniers km / h
gagnés par le T.G.V., par exemple, coûtent cher.
|
Chute libre d'initiation en tamdem.
Début de chute 3 600 m. Fin de chute
1 500 m. Durée 45 s.
|
|
Compétition entre 2 forces: le poids, constant,
et la résistance de l'air qui augmente avec la vitesse et qui s'oppose
au poids. On s'attend donc, à plus ou moins longue échéance, à
une égalité entre ses 2 forces, à une résultante nulle, à
une accélération nulle et donc à une vitesse constante. Au cours
de ce saut, nous allions, au bout de 8 secondes environ, à 55 m/s
soit 200 km/h. Le photographe, parti en même temps, va à la même
vitesse.
|
|
c - Poussée d'Archimède de l'air:
|

|
négligée car
|

|
L'air a une masse volumique au sol d'environ 1,3 kg/m3
alors que les corps dont nous étudions le mouvement ont des masses volumiques
de l'ordre de 1000 kg/m3 ou plus.
E - Relation fondamentale de la Dynamique - L'accélération:
Si le système choisi était le système "Terre + projectile",
le poids ne serait pas une force extérieure.
La masse se simplifie car c'est la même masse qui fait le
poids du projectile et son inertie au mouvement.
On obtient l'équation différentielle vectorielle suivante:

L'accélération est indépendante du temps. Elle est égale à
- g ( avec l'orientation de Oz vers le haut).
Elle dépend donc, comme g, de l'altitude et de la latitude
terrestres.
Elle dépend aussi de la masse de l'astre attracteur ( Lune,
Soleil, Planète...) et,
au voisinage de cet astre, de l'altitude et de la latitude.
En intégrant , il ne faut pas oublier les constantes
qui pourront être déterminées grâce aux conditions initiales imposées
par la situation::

F - Première intégration - La vitesse:

Il y a deux invariants dans ce mouvement:
- la vitesse vy suivant l'axe Oy: initialement nulle,
elle reste nulle, cela signifie que le projectile reste dans le plan xOz. On
peut maintenant passer sous silence ce qui se passe hors du plan xOz.
- la vitesse vx (composante horizontale) suivant
l'axe Ox est constamment égale à v0 cos  .
.
En effet, la force ( le poids ) a une composante nulle suivant
Ox et suivant Oy: il ne peut donc y avoir de variation de vitesse suivant
ces 2 axes.
Par contre la vitesse vz (composante verticale)
dépend du temps t. ( le poids a sa composante verticale non nulle
).
|
vz est positive
|

|
Le projectile s'élève puisque Oz est dirigé vers
le haut.
|
|
vz s'annule à l'instant
|

|
Le projectile culmine.
|
|
vz est négative
|

|
L'altitude du projectile diminue avec le temps.
|
Comportement de la vitesse et de ses composantes vx
et vz.
L'angle  que fait la direction de la vitesse avec l'axe horizontal Ox vaut
que fait la direction de la vitesse avec l'axe horizontal Ox vaut  à l'instant 0 mais d'une façon générakle, à l'instant générique
t:
à l'instant 0 mais d'une façon générakle, à l'instant générique
t:

Bientôt, on comprendra mieux la signification particulière
de cet instant. C'est l'instant où le projectile, parti d'une altitude z0
( éventuellement 0 ), repasse par la même altitude z0 (
éventuellement 0 ).
La norme de la vitesse dépend, elle-aussi, du temps:
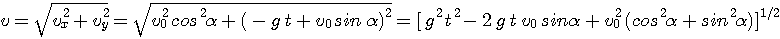


|

|
date du lancement.
|
|

|
instant où le projectile a la même altitude qu'au
lancement.
|
G - Deuxième intégration - La loi horaire du mouvement
- L'équation paramétrique de la trajectoire:
Reprenons la solution

|
à l'instant t = 0:
|

|
d'où la loi horaire du mouvement:
|
|
Mouvement rectiligne et uniforme de la projection
orthogonale du projectile sur l'axe Ox.
|
|
La trajectoire est plane, contenue dans le plan
xOz.
|
|
Comportement parabolique de la côte (ou altitude
) z.
|
Cette loi horaire est encore appelée équation paramétrique de
la trajectoire ( le paramètre étant le temps ) car en se donnant t, on peut
calculer x et z correspondants et trouver l'ensemble des points par où passe
le projectile.
H - Equation cartésienne z ( x ) de la trajectoire:
Reprenons l'équation paramétrique:

Eliminons le temps t dans la ligne 3 en l'exprimant grâce
à la ligne 1:

qui, injectée dans 3, donne l'équation cartésienne de la trajectoire:
C'est une parabole à concavité tournée vers le bas ( coeff.
de x2 < 0 et axe Oz vers le haut ).

Le quotient est en mètres: le premier terme du second membre
est bien homogène à une longueur.
Expérience à la maison:
Webcam - 25 images par seconde - Pose 1/250 s - Règle
de 30 cm.
I - Calcul de la flèche h:
1°) Utilisation de tS :

Elle est maximale pour  = 90°.
= 90°.
2°) Utilisation de la dérivée dz / dx:
on exprime d'abord l'abscisse xS du sommet de la
parabole.

Il vient:
Maximum pour 
|
Ensuite on injecte
|

|

|
On a:
J - Calcul de la portée:
Soit C le point où le projectile percute le sol. La portée
est OC. C est l'intersection de la trajectoire du projectile et de la droite
z = 0 soit

Maximum pour  .
.
K - Variante 1:
Le projectile part de l'altitude z0 différente de
zéro. Il faut reprendre à partir de la condition initiale qui porte sur z.
Tout ce qui précède ( accélérations, vitesses, x ( t ) et y(
t) ) reste inchangé. Seule change z ( t ).
A l'instant t = 0, z n'est plus égal à 0 mais à z0;
la constante Cste3 est alors égale à z0 d'où la nouvelle loi horaire:

L'instant de passage en S est le même. La flèche est augmentée
de z0.
Plus difficile est le calcul de la portée. Il faut résoudre
l'équation du second degré:

|

|
avec
|

|
soit ici,
L - Variante 2 - Terrain en pente:
Le terrain ( montant ou descendant ) peut être représenté
par la droite z = z'0 ± a . x ou encore z
= z'0 ± x . tan 

Pas de grosse difficulté supplémentaire, il suffit de résoudre

pour obtenir l'abscisse du point d'impact.
Voir
l'animation virtuelle

 un objet non chargé de masse m constante dans une région assez
petite pour que l'intensité de la pesanteur puisse être considérée
comme constante.
un objet non chargé de masse m constante dans une région assez
petite pour que l'intensité de la pesanteur puisse être considérée
comme constante. et de la façon suivante:
et de la façon suivante:
 l'angle orienté
l'angle orienté  .
. , vertical, dirigé vers le bas, de norme:
, vertical, dirigé vers le bas, de norme:









 .
.


 que fait la direction de la vitesse avec l'axe horizontal Ox vaut
que fait la direction de la vitesse avec l'axe horizontal Ox vaut  à l'instant 0 mais d'une façon générakle, à l'instant générique
t:
à l'instant 0 mais d'une façon générakle, à l'instant générique
t:



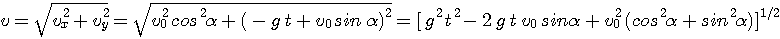




















 = 90°.
= 90°.













 .
.







