TP - EXAO - Décharge oscillante dans un circuit RLC série
1. Montage pour étudier uc(t) et visualiser les 3 régimes libres:
Inverseur en position 1: charge quasi-immédiate ( R = 0 ). Inverseur en position 2: le condensateur se décharge dans le dipôle RL.
Pour
t 
0,
le régime est dit libre car il n’y a plus d’apport d’énergie.
2. Résultats en E.X.A.O.:
Régime sinusoïdal amorti - L'amortissement augmente avec la résistance.
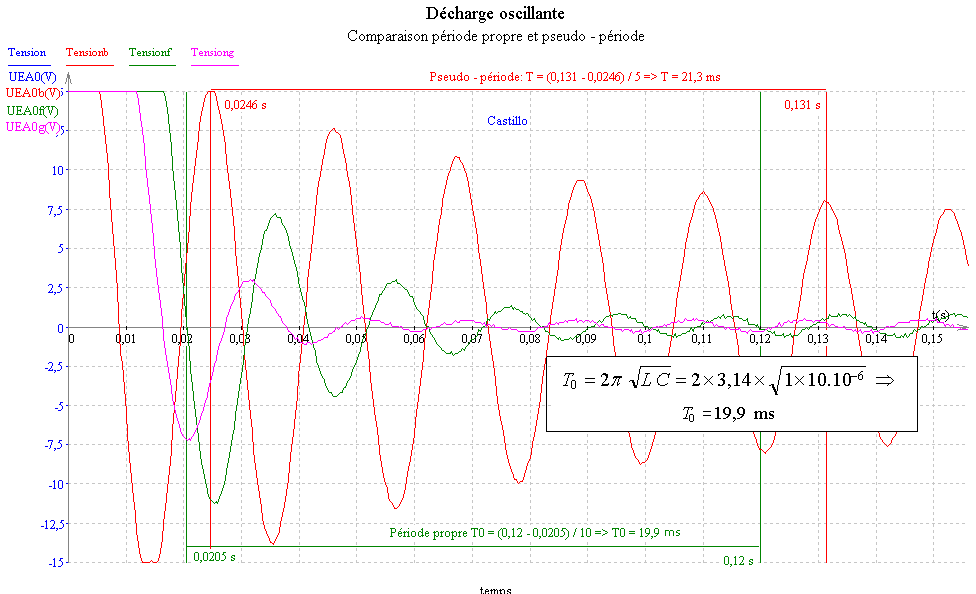
La période et la pseudo-période sont sensiblement égales.
2 des 3 types de régimes.
3. Résultats de simulation avec Crocodile Physics:
4. Équation différentielle: la loi des mailles: uL + uR + uC = 0 =>
|
|
|
RT/L s'appelle terme d'amortissement.
5. Cas où RT = 0: (bobine idéale et résistance additionnelle nulle)
La fonction est proportionnelle à sa dérivée seconde comme les fonctions sinus, cosinus ou exponentielle mais elle est de signe opposé comme seules les fonctions sinus ou cosinus. Cherchons donc des solutions de la forme uc(t) = A cos (ωo t + φ).
* A s'appelle l'amplitude des oscillations tandis que 2 × A est l'amplitude crête à crête.
* ωo est la pulsation.
* ωo t + φ est la phase à l'instant t tandis que φ est la phase à l'origine des temps.
On vérifie la plausibilité de cette solution. En effet,
u'c(t) = - ωo A sin (ωo t + φ) et u"c(t) = - ωo2 A cos (ωo t + φ)
=> u"c(t) = - ωo2 uc(t)
Utilisons les conditions initiales pour déterminer A et φ. Celles-ci sont : uc(0) = Uo, q(0) = C Uo et i(0) = 0.
i = C u'c => i = - ωo C A sin (ωo t + φ).
Or i(0) = 0 => - ωo C A sin φ = 0
Donc φ = 0 à k π près.
On a donc uc(t) = A cos (ωo t) et comme, de plus, uc(0) = Uo, A = Uo
D'où uc(t) = Uo cos (ωo t) et un comportement sinusoïdal.
Relation entre pulsation, période propre To et fréquence propre fo:
À l'instant t = 0, la phase (ωo t) vaut zéro radian. Au bout d'une période To ( t = To) ,
elle vaut 2 π radians => ωoTo = 2 π =>
ou encore:
On peut donc écrire uc(t) sous la forme:
6. Animation intéractive:
|
|
|
|
