1°) Grandeurs électriques:

- vecteur densité de courant:

- intensité du courant:

- équation de conservation de la charge:

- loi d'ohm microscopique:

d'où l'équation différentielle de son mouvement:

qui a pour solution:

soit, pour des dates grandes par rapport à m/k mais petites pour nos moyens d'investigation,

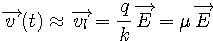
où est la mobilité de la charge électrique. Le vecteur densité de courant atteint, lui, la valeur limite:

où n ( n en m^-3 ) est la densité particulaire des porteurs de charge q.

qui est la loi d'ohm microscopique.

est la conductivité électrique du milieu, inverse de sa résistivité ( attention ) elle-aussi notée souvent .

- résistances de conducteurs ( ici est la résistivité en ):

est la conductance du tronçon conducteur et s'exprime en siemens ( S ).

est une loi d'ohm macroscopique.

- loi de Joule:

la charge dq, soumise à la force

échange la puissance

( loi de Joule microscopique )

Dans le volume V, cette puissance vaut:

( loi de joule macroscopique ).

Pour un conducteur qui suit la loi d'ohm U = R I,

- récepteurs et générateurs:

soit un dipôle ( D ) attaqué par une tension u et répondant par un courant I

Convention d'orientation récepteur.

Si P > 0, le dipôle reçoit de l'énergie: il est dit récepteur. Si P < 0, le dipôle est générateur. Exemples: pour une résistance, P = u I = R i² >0 (récepteur) et pour une pile, u = r i - e (conv. récepteur):