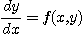
Méthode d'Euler - Chute dans un fluide
1. Notes mathématiques:
Une équation différentielle est une expression reliant une fonction y (x) et ses différentes dérivées successives.
Résoudre l'équation différentielle, c'est trouver la fonction y (x).
Soit une fonction y (x) dont la dérivée est connue qui obéit à l'équation différentielle suivante:
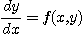
Si l'on connait la valeur y0 de y pour une valeur x0 de x, alors f ( x0,y0 ) est connue ainsi que
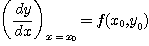
Il est alors possible de connaître la valeur y1 de y pour une valeur x1 de x voisine de x0
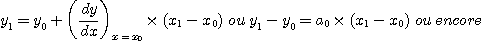
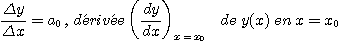
De même, on pourra connaître une valeur y2 de y lorsque x prend la valeur x2.
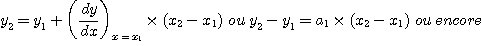
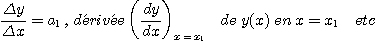
Ainsi, grâce à la connaissance de la dérivée y'de y, on peut, de proche en proche, évaluer les différentes valeurs yi de y (x).
C'est la méthode d'Euler, méthode itérative encore désignée comme méthode d'intégration numérique.
C'est une méthode utilisée principalement lorsqu'une équation différentielle n' a pas de solution analytique, c'est à dire lorsque la solution n'est pas une fonction simple ou une somme finie de fonctions simples. Par exemple le mouvement de trois corps en influence gravitationnelle mutuelle, n'a pas de solution analytique. On ne peut le résoudre que par approximations successives mais ceci marche très bien puisqu'on a pu découvrir (par exemple) la planète Neptune par le calcul.
Exemples d'équations différentielles en Sciences Physiques:
|
Population N(t) d'atomes radioactifs qui se désintègrent progressivement |
Concentration C(t) d'un réactif chimique qui diminue au cours du temps |
Accélération a(t) = dv/dt qui diminue à cause de forces de frottements fluides |
|
|
|
( g > g' intensité apparente de la pesanteur ) |
2 Réalité, observable, modélisation:
Dans une expérience physique nous sommes confrontés au réel, à l'observationnel et à la modélisation:
|
3. Chute dans un fluide visqueux:
Le poids apparent est le poids réel diminué de la Poussée d'Archimède.
Expression de l'intensité apparente g' de la pesanteur:
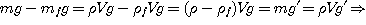
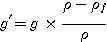
Il faut connaître les 2 masses volumiques (corps en chute et fluide). Voir un tableau de masses volumiques.
Exemple pour une bille en acier (7 800 kg.m-3) qui tombe dans l'eau (1 000 kg.m-3 )
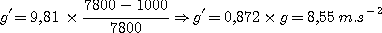
|
Equation différentielle du mouvement:
|
|
|
Pour calculer k/m on peut utiliser la vitesse limite vl si elle est accessible; en effet, lorsque cette vitresse est atteinte, l'accélération est nulle:
|
|
|
|
|
Ainsi; par exemple, si la vitesse limite vaut 0,95 m.s-1, comme dans l'acquisition ci-dessus,
|
|
|
|
Orientation vers le bas:
|
t(ms) |
L'accélération dv/dt en m.s-2 |
La vitesse v(t) en m.s-1 |
La position x(t) en m. |
|
Pas de 33 ms |
|
|
|
|
t0 = 0 |
a0 = 8,55 |
v0 = 0 |
x0 = 0 |
|
t1 = 33 |
a1 = 8,55 - 9,47*02 = 8,55 |
v1= 0 + 8,55 * 0,033 = 0,282 |
x1 = 0 + 0* 0,033 = 0 |
|
t2 = 67 |
a2 = 8,55 - 9,47*0,2822 = 7,80 |
v2 = 0,282 + 8,55*0,033 = 0,564 |
x2 = 0 + 0,282* 0,033 = 0,282 |
|
t3= 100 |
a3 =8,55 - 9,47*0,5642 = 5,54 |
v3 = 0,564 + 7,80*0,033 = 0,821 |
x3 = 0,282 + 0,564* 0,033 = 0,301 |
|
t4 = 133 |
a4 =8,55 - 9,47*0,8212 = 2,17 |
v4 = 0,821 + 5,54*0,033 = 1,00 |
x4 = 0,301 + 0,821* 0,033 = 0,328 |
|
t5 = 167 |
a5 =8,55 - 9,47*1,0002 = - 0,92 (stop) |
v5 = 1,00 + 2,17*0,033 = 1,07 |
x5 = 0,328 + 1,00* 0,033 = 0,361 |
Fichier excel à lire ou à télécharger.
|
|