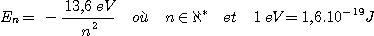
Spectre lumineux de l'hydrogène monoatomique H

Energie de l'électron dans l'atome H ( pas le dihydrogène H₂ ): elle est donnée par l'expression:

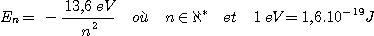
n est le nombre quantique principal, il désigne le numéro de la couche électronique dans laquelle se situe l'électron. L'énergie ne peut prendre que certaines valeurs (à la différence des planètes et satellites): on dit qu'elle est quantifiée.

Ce sont des états liés de l'électron au noyau. Attention, le premier niveau d'énergie (niveau fondamental) est parfois noté E₀.

Lorsque n --> 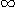l'électron est non lié ou encore libre, l'atome H est ionisé. E = 0. L'électron est au repos. Pour des valeurs de E >0, l'atome est ionisé et l'électron en mouvement, doté d'une énergie cinétique non nulle.

Diagramme d'énergie de l'atome d'hydrogène: Reportons ces différentes énergies dans le diagramme suivant:

Les niveaux de n croissants sont de plus en plus rapprochés et on a presque un continuum lorsque n ---> .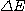

Lorsque l'atome gagne ou perd de l'énergie 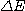,au cours d'un choc par exemple, l'électron change de niveau. Il faut que 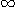soit exactement égale à la différence d'énergie entre 2 niveaux possibles, sinon l'échange d'énergie ne se fait pas.

Emission et absorption de lumière lors d'un saut électronique:

Le gain d'énergie peut se faire si l'atome absorbe une radiation lumineuse de fréquence     ou de longueur d'onde l (dans le spectre de la lumière éclairant l'atome, on aura une raie sombre sur fond brillant et le spectre de la lumière reçue sera un spectre de raies d'absorption).

L'émission de lumière peut se faire, par perte d'énergie de l'électron, si l'électron passe d'un niveau excité à un niveau de plus basse énergie: raie brillante sur un fond sombre et on aura un spectre de raies d'émission.

h = 6,63.10^-34 m².kg.s^-1 ( ou J.s) est la constante de Planck, c est la célérité de la lumière dans le vide c = 3,00.10⁸ m.s^-1. DE doit être en joules si l'on veut la longueur d'onde en mètres.

On note qu'un atome peut absorber les mêmes fréquences lumineuses que celles qu'il peut émettre (même 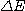). Le saut de l'électron ne se fait pas obligatoirement sur le niveau immédiatement voisin.

Niveaux d'énergie et émission de lumière par l'atome H

On voit que le spectre d'émission (ou d'absorption ) de l'hydrogène présente de nombreuses raies groupées par séries.

Lorsque la transition électronique aboutit sur le niveau fondamental (n = 1), c'est la série de Lyman, elle se trouve dans le domaine U.V..

Lorsque la transition électronique aboutit sur le premier niveau excité (n = 2), c'est la série de Balmer, elle se trouve en grande partie dans le domaine visible.

Lorsque la transition électronique aboutit sur le deuxième niveau excité (n = 3), c'est la série de Paschen, elle se trouve dans le domaine I.R..

Calcul de la longueur d'onde de la raie Ha (émise ou absorbée): elle correspond à la transition du niveau n = 3 au niveau n = 2 et inversement. On écrit que l'énergie 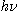   du photon échangé est égale à .

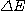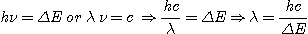
h = 6,63.10^-34 m².kg.s^-1 est la constante de Planck, c est la célérité de la lumière dans le vide c = 3,00.10⁸ m.s^-1. 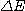doit être en joules et on obtient la longueur d'onde en mètres.

Dans notre cas l'électron passe du niveau 3 au niveau 2 ou inversement et il émet ou il absorbe une radiation de longueur d'onde:

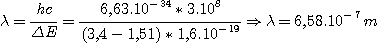
Soit 658 nm: c'est une raie rouge, c'est la raie rouge baptisée Ha des nébuleuses, lesquelles contiennent principalement de l'hydrogène atomique. Les nébulosités bleues sont généralement dues à la réflexion de la lumière sur les grains de poussière des nébuleuses.

  Nébuleuse d'Orion - Distance 2 000 années-lumière - Flat Field Camera- Diamètre 20 cm- Distance focale 760 mm-

Pose de 20 min sur film Fuji 200 ASA hypersensibilisé.

 Quelques raies du spectre de l'hydrogène atomique: Comme le calcul est répétitif, utilisons la formule semi-littérale suivante:

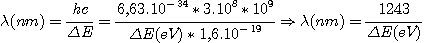
Résultats pour les 3 premières séries:

Plaçons ces quelques raies dans le spectre de l'hydrogène atomique:

 Formule de Ritz et constante de Rydberg : exprimons 1 / l , l étant la longueur d'onde, en mètres, de la radiation émise ou absorbée lors de la transition entre le niveau n et le niveau m, n et m étant des nombres entiers naturels non nuls .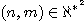

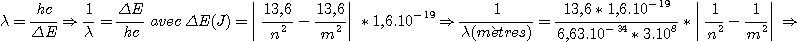
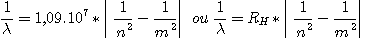
Cette dernière expression est la formule de Ritz. La constante R_H = 1,09.10⁷ est la constante de Rydberg, elle a la même unité que 1 / l et s'exprime donc en m^-1.

 1 / l  représente le nombre de longueurs d'onde par mètre et est appelé nombre d'ondes. Si l'on veut calculer l , on a les 2 choix suivants:
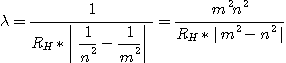