Oscillations mécaniques d'un ressort horizontal
Modèle grossier de vibrations dans les molécules diatomiques
A - Le ressort au repos - Raideur k du ressort:
|
La définition de k vient tout naturellement, une fois constatée expérimentalement la proportionnalité entre l'allongement x et la masse M accrochée au ressort.
B - Le ressort en mouvement :
Soit une masse m qui peut coulisser sans frottement sur un rail horizontal.
|
|
Accrochons à cette masse un ressort de raideur k.
Ecartons d'une distance Xm le point G de sa position d'équilibre ( choisie comme origine O ) puis lachons la masse. Elle se met à osciller horizontalement, guidée par le rail. Choisissons un axe Ox horizontal. Soit x = OG ( algébriquement ) l'abscisse du point G. Adoptons comme instant zéro celui où l'on lache la masse.
A l'instant zéro, nous avons donc les conditions initiales:
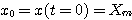
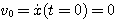
C - Système = Masse m:
D - Référentiel terrestre supposé galiléen:
E - Bilan des forces extérieures:
- le poids , vertical, dirigé vers le bas, d'intensité P = m g
- la réaction du rail, verticale car on néglige les frottements ( donc pas de composante horizontale), dirigée vers le haut, d'intensité R égale à P. La réaction s'ajuste à la valeur de P.
- la tension du ressort, horizontale, d'intensité proportionnelle à l'allongement du ressort, de valeur algébrique opposée à celle de OG.
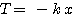
On remarquera que OG n'est pas l - l0 ( au sens des définitions ) mais qu'il est égal à l - l0.
Tant qu'on n'a pas laché le ressort, il y a la force musculaire de l'opérateur, opposée à la tension du ressort.
F - Relation fondamentale de la Dynamique - L'accélération:
|
|
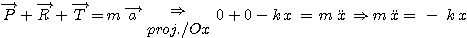
d'où
|
|
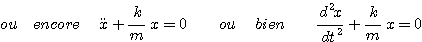
L'accélération n'est pas constante, elle dépend de l'élongation x du point G. Elle est nulle en même temps que x c'est à dire lorsque G passe par sa position d'équilibre. Sa valeur absolue est maximale lorsque l'élongation est maximale.
G - Recherche de solutions x ( t ):
Cherchons des solutions sinusoïdales du temps, c'est à dire de la forme:
|
|
est l'élongation du point G à l'instant t. |
|
|
est l'amplitude du mouvement vibratoire. |
|
|
|
est la pulsation (en rad.s-1). |
|
|
|
est la phase du mouvement à l'instant t. |
|
|
|
est la phase à l'origine des temps. |
Attention au mode calculatrice!
Nous avons 2 arguments à celà:
- la forme de l'enregistrement de l'élongation en fonction du temps.
- la dérivée seconde d'une fonction sinusoïdale est proportionnelle à cette dernière fonction et a un signe opposé.
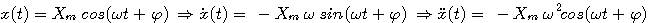
soit
|
|
identique à |
|
à condition de poser |
|
La pulsation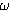 
est aussi la vitesse angulaire du vecteur tournant de Fresnel qui représente
le mouvement de G.
La loi horaire
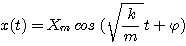
est donc solution de l'équation différentielle qui régit le mouvement de la masse m.
Pour exprimer la phase à l'origine des temps, utilisons la condition initiale x ( 0 ) = Xm:
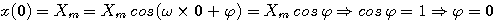
d'où la loi horaire:
|
|
x ( 0 ) = Xm.
x(t) reprend la même valeur Xm périodiquemant ( fonction cosinus ) lorsque
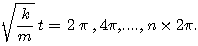
La plus petite de ces dates est la période T. Elle est telle que:
|
|
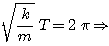
Plus le ressort est raide, plus la période est courte.
Plus la masse est inerte, plus la période est grande.
La fréquence ( en Hz ) est inversement proportionnelle à la période:
|
|
H - Déphasage entre les grandeurs cinématiques:
|
Elongation |
Vitesse |
Accélération |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
en quadrature avance sur x(t). |
en opposition de phase avec x(t), en quadrature avance sur v(t). |
Voir l'oscillateur amorti et entretenu dans les pages Sup-Spé-DEUG
|
|
|
|
