Remarque: la tension du fil, perpendiculaire à la trajectoire, ne travaille pas.
|
|
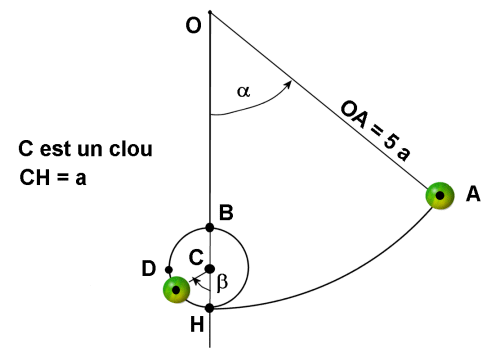
Différentes possibilités de mouvements: 4 au moins;
le corps tombe en chute libre suivant la verticale jusqu'à ce que le fil soit tendu
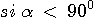
a) si la vitesse acquise en H est suffisante, le corps peut tourner autour du point C selon un mouvement quasi-circulaire non uniforme.
b) Pour une certaine valeur de la vitesse acquise en H et inférieure à la précédente, le corps atteint et dépasse le point D, il s'immobilise puis retombe en chute libre suivant la verticale.
c) Pour une valeur de la vitesse acquise en H encore inférieure à celle du cas précédent, le corps n'atteint pas le point D, fait une demi-oscillation autour de C puis dépasse le point H.
Energie des pendules pesants
En A, le corps a une énergie mécanique Em
qui se réduit à sa seule composante potentielle Em
= m g l ( 1 - cos 
), soit
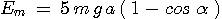
Lorsque le fil bute sur le clou et que le pendule a alors une
longueur a et une élongation angulaire maximale ou amplitude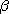 
, l'énergie mécanique, inchangée, a pour expression
Em = m g l ( 1 - cos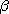 
), soit
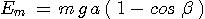
Condition pour atteindre le point B:
Pour que le corps atteigne le point B, il faut que 
= 
, soit
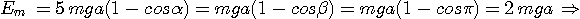
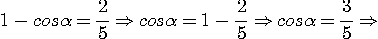
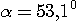
Le corps arrive en ce point B sans vitesse et retombe sur le clou, en chute libre suivant la verticale. Le fil ne s'enroule pas autour du clou.
Condition pour que le fil s'enroule autour du clou:
Pour que le fil s'enroule, il faut que la tension de ce fil ne soit pas nulle lors du passage en B. Ecrivons la deuxième loi de Newton, dans le référentiel terrestre supposé galiléen:
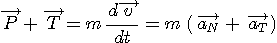
( attention confusion possible entre l'accélération a et la longueur a du fil )
soit, en projetant vers le bas ( seule aN intervient et l'on connait son expression v2/R pour un mouvement circulaire ),
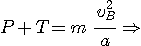
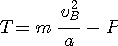
On veut T > 0, il vient donc:
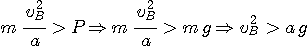
C'est la condition pour que le fil reste tendu au passage en B. Explicitons cette relation:
En B le corps a une énergie mécanique
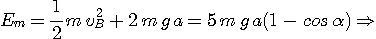
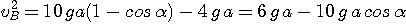
et l'on doit avoir
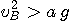
On tire
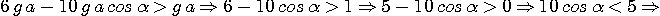
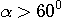
Le fil s'enroule alors autour du clou.
|
|
|
|
