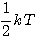
Instabilité gravitationnelle
Nous cherchons à quelle condition sur sa masse (critère de Jeans) un nuage interstellaire sphérique se contracte pour donner naissance à une ou plusieurs étoiles.
Nous considérons d'abord un nuage d'hydrogène monoatomique H ( régions HI ou HII ) puis nous verrons la légère modification apportée s'il s'agit d'hydrogène diatomique H2 (nuages moléculaires).
1. Énergie totale du nuage:
Au début de sa contraction nous supposons le nuage de gaz homogène et isotherme, de rayon R, constitué de N atomes d'hydrogène quasi-ponctuels, ayant chacun 3 degrés de liberté (translation).
a) énergie cinétique ou thermique:
L'énergie cinétique vaut
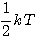
par degré de liberté et par particule.
Les particules monoatomiques (H ou He) ont 3 degrés de liberté de translation. Il y a N particules en tout.
D'où l'énergie cinétique totale:
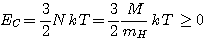
en notant mH la masse de l'atome d'hydrogène.
b) énergie potentielle gravitationnelle:

|
et comme: |
|
on a |
|
d'où |
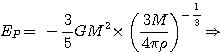
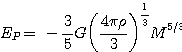
2. Condition d'effondrement:
L'énergie cinétique, qui pousse à la dilution du nuage, est proportionnelle à la masse, tandis que l'énergie potentielle, qui traduit le confinement gravitationnel est, elle, proportionnelle à la puissance 5/3 de cette masse.
On peut donc prévoir que si la masse est suffisamment grande et si elle dépasse un certain seuil (masse de Jeans), l'énergie potentielle (< 0) l'emportera sur l'énergie cinétique (> 0) et le nuage se contractera inexorablement. Cette masse critique est appelée masse de Jeans.
Lorsque cette masse est dépassée, l'énergie totale du nuage est négative:
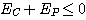
Prenons le cas limite:
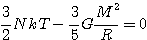
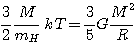
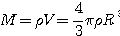

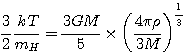
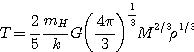
Inversement,
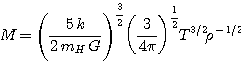
|
|
• Application semi-numérique:

|
|
Autre forme de l'équation en remplaçant:
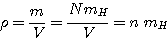
n étant la densité particulaire N/V
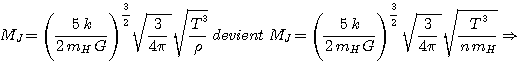
|
|
• Application semi-numérique:
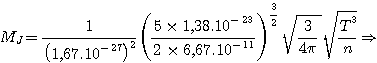
|
En fonction de la masse du Soleil:
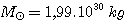
|
3. Cas d'un nuage moléculaire de dihydrogène:
Les molécules diatomiques (H2 des nuages moléculaires, CO...) ont 3 degrés de liberté de translation et 2 degrés de liberté de rotation soit 5 degrés de liberté en tout.
On peut négliger les niveaux de vibration dont les quanta sont beaucoup plus élevés et ne sont pas concernés à ces températures.
Autrement dit, à ces températures, les niveaux de vibration ne sont pas atteints et les molécules ne vibrent pas.
On a donc 5 degrés de liberté pour N particules diatomiques:
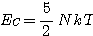
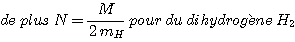
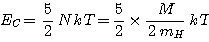

Coefficient 5/4 = 1,25 pour (H2) au lieu de 3/2 = 1,5 pour (H), cela ne change donc pas grand chose.
En utilisant l'expression établie plus haut:
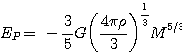
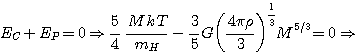
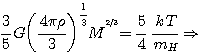
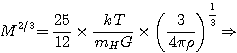
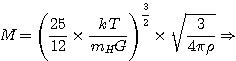
|
|
Coefficient (25/12)3/2 = 3,0 pour H2, au lieu de (5/2)3/2 = 3,95 pour H.
• Application semi-numérique:
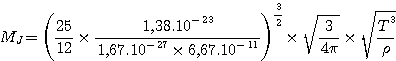
|
|
Si on préfère faire intervenir la densité particulaire n,
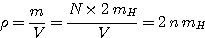
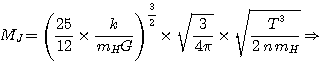
|
|
• Application semi-numérique:
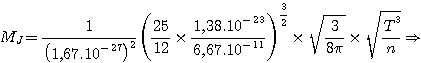
|
Soit, en masse solaire (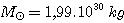 ),
),
|
|
4. Exemples:
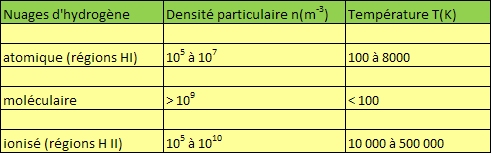
Sous le radical, la température intervient au cube et rend ces régions inégalement fécondes quant à la possibilité d'effondrement et à la formation d'étoiles, la palme allant aux nuages moléculaires.
Par exemple avec (50 K et 109 m-3) dans un nuage moléculaire:
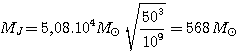
Calculons le rayon du nuage:
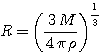
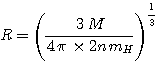
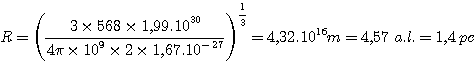
Les régions HII conduisent à des masses prohibitives quant à cette instabilité gravitationnelle.
Par exemple avec (100 000 K et 107 m-3):
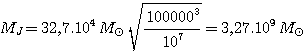
et le rayon:
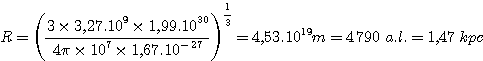
5. Fractionnement du nuage:
Au cours de la contraction, la densité particulaire n augmente et la masse critique: |
|
diminue, elle devient inférieure à la masse initiale du nuage. |
Il s'ensuit que le nuage est susceptible de se fractionner en plusieurs morceaux et de donner naissance à un amas d'étoiles.