A - Principe de Fermat - Conséquences:

- célérité de la lumière dans le vide:

voir un tableau des constantes de la Physique

- indice de réfraction d’un milieu:

n est sans unité, il dépend de la couleur de la lumière, plus généralement de la longueur d'onde de l'onde électromagnétique.

- chemin optique élémentaire dL:

soit dl,  de milieu M, un élémentd'un rayon lumineux. Par définition:

- signification:

distance que parcourrait la lumière dans le vide pendant la même durée.

- principe de Fermat:

le trajet réellement suivi par la lumière pour aller d’un point A à. un point B est celui pour lequel le chemin optique est extrêmal ou station naire par rapport aux trajets infiniment voisins.

- traduction physique:

- conséquence 1:

milieu homogène n ( M ) invariant de lieu

Le plus court chemin est le trajet rectiligne AB. Dans un milieu homogène, les rayons sont des segments.

- conséquence 2:

lois de Descartes pour la réflexion et pour la réfraction

- soit (  ) un dioptre, c'est à dire une surface séparant deux milieux d'indice de réfraction n₁ et n₂ différents.

- 1 est le rayon incident, 3 est le rayon réfléchi, 2 est le rayon réfracté.

- I est le point d'incidence.

- ( N ) est la normale en I au dioptre.

- ( ) est le plan tangent en I au dioptre.

- le rayon incident et la normale ( N ) définissent le plan d'incidence.

- i₁, i₂, i₃ sont les angles d'incidence, de réflexion, de réfraction. Ils sont orientés à partir de la normale.

cas de la réfraction

Pour un trajet  de A1 à A2 infiniment voisin du précédent et passant par le point d'incidence I', infiniment voisin de I, le chemin optique varie de dL:

d'où

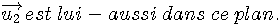
Le rayon réfracté est dans le plan d'incidence

(1^ère loi de Descartes pour la réfraction).

D'autre part, formons

(2^ème loi de Descartes pour la réfraction)

Les indices de réfraction sont inférieurs à 3 donc si i₁ est petit, i₂ l'est aussi et on obtient la loi de Kepler:

cas de la réflexion

Sur le trajet A₁IA₃  pour lequel n₁ = n₃

le rayon réfléchi est dans le plan d'incidence

(1^ère loi de Descartes pour la réflexion).

(2^ème loi de Descartes pour la réflexion)

Dispositif d'étude de la réflexion et de la réfraction