T1- Dans un domaine de pressions, l’équation d’état d’un gaz est:

où B ne dépend que de la température T.

Exprimer le coefficient de dilatation à pression constante et le coefficient de compressibilité isotherme du gaz.

Voir ou télécharger la correction ( par Geneviève GOMI, étudiante )

T2- Un gaz obéit à l'équation de Van der Waals:

où a et b sont des constantes.

Montrer que

et que

T3- Quelle augmentation de pression faut-il exercer sur un liquide ou sur un solide pour supprimer sa dilatation lors d'une élévation de température T.

Voir ou télécharger la correction ( par Geneviève GOMI, étudiante )

T4- a) exprimer en fonction de et de le travail reçu par un système au cours d’une transformation élémentaire réversible en fonction de dP et de dT.

b)   examiner le cas particulier du travail reçu lors d’une compression finie et isotherme lorsque et sont supposés constants (solides ou liquides).

T5- Un solide passe d’un état A à un état C:

a) au moyen d’une transformation ABC.

b) au moyen d’une transformation AC caractérisée par P = P₀ + a T. Calculer le travail W_AC dans les 2 cas en supposant V, 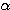et constants.

T6- Expérience et méthode de Clément et Desormes:

Un grand ballon fermé par un robinet contient un gaz parfait sous une pression initiale P_i = P₀ - h.  P₀ est la pression

extérieure et h l’indication d’un manomètre à mercure.

On ouvre brusquement le robinet puis on le referme. Le gaz subit alors une compression sensiblement adiabatique et

réversible, suivie d’un refroidissement à volume constant ( la variation de volume du ballon peut être négligée).

A la fin du refroidissement la pression du gaz est devenue: P_f  = P₀ - h’. Exprimer = C_p/C_v en fonction de h et de h’.

T7- Exprimer la pression en fonction de l’altitude dans l’atmosphère supposée se comportant comme un gaz parfait à

température constante.

La pression au sol étant P₀, pression atmosphérique normale , et la température étant de 20°C, calculer l’altitude à laquelle la

pression est réduite à P₀/10. On suppose g indépendant de l’altitude, égal à 9,81.m.s^-2.

T8- L’atmosphère est maintenant supposée adiabatique, vérifiant la relation:

Au sol, pression = P₀ , température = 20 °C, g = 9,81  m.s^-2 et   = 1,4.

Calculer à quelle altitude la pression vaut P₀/10.

T9- Calculer la masse volumique de la vapeur d’eau à 100 °C considérée comme un gaz parfait.

T10- Un litre d’oxygène( O₂ = 32 g.mol^-1) à 20°C sous 3.10⁵ Pa et 3 litres de dioxyde de carbone (CO₂ = 44 g.mol^-1) à

50°C sous 2.10⁵ Pa sont mélangés dans un récipient de volume 5 litres à 40 °C. Calculer la pression et la masse molaire du

mélange.

Voir ou télécharger la correction ( par Geneviève GOMI, étudiante )