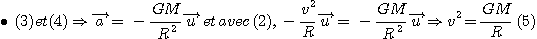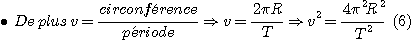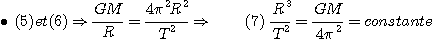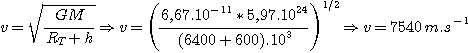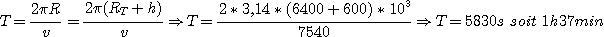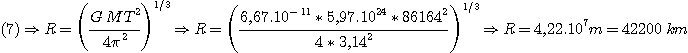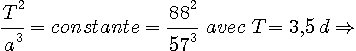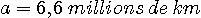La
3ème loi de Kepler et le mouvement circulaire uniforme
Rappelons cette loi: Pour toutes les planètes, le rapport entre le cube du demi grand axe de la
trajectoire et le carré de la période de révolution est le même.
Nous considérons des astres (planètes, satellites
naturels, étoiles...) ou des satellites artificiels qui tournent autour
d'un autre astre (le même) avec un mouvement circulaire et uniforme. Dans
le cas de figure suivant, S est le Soleil et P une planète.
|

|
 SP = R, rayon de l'orbite circulaire est, dans ce cas, le demi grand axe.(On
l'appelle parfois le rayon vecteur). SP = R, rayon de l'orbite circulaire est, dans ce cas, le demi grand axe.(On
l'appelle parfois le rayon vecteur).
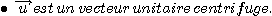

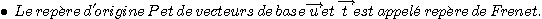
Ce n'est pas un repère galiléen, mais
une fois qu'on a appliqué la deuxième loi de Newton
dans un repère galiléen (héliocentrique, non
représenté sur le dessin) on peut utiliser le repère
de Frenet pour projeter cette 2ème loi de Newton.
 Nous avons vu les relations suivantes: Nous avons vu les relations suivantes:

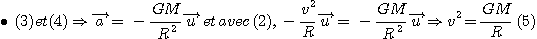
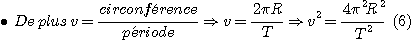
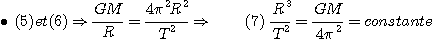
|
Le cube du demi grand axe est bien proportionnel au carré
de la période de révolution. Ceci lorsque l'astre situé
au centre du cercle est le même puisqu'il y a le terme M dans la constante.
On note que le résultat est indépendant de la masse de la planète,
ainsi, si la planète Jupiter (380 fois plus massive que la Terre) tournait
à la place de la Terre, elle aurait une période de révolution
de 1 année.
Note 1: Calculons
la vitesse et la période de révolution d'un satellite en orbite
basse, disons h = 600 km d'altitude. Données: le rayon de la Terre RT
= 6400 km, masse de la Terre M = 5,97.1024 kg, constante de
la gravitation G = 6,67.10-11 N.m2.kg-2. De
la relation (5) et en remarquant qu'ici R = RT + h, on
déduit la vitesse (une erreur fréquente est d'oublier la conversion
des km en m et de ne pas prendre la racine carrée...)
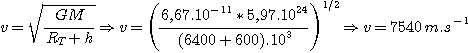
Calculons maintenant la période de révolution
T:
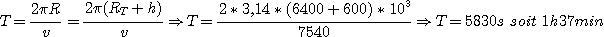
Note 2: Cas des satellites géostationnaires.
Pour qu'un satellite soit fixe par rapport à la Terre, son orbite doit
être circulaire et dans le plan équatorial de la
Terre et il faut que sa période de révolution autour
de notre planète soit égale à la période de rotation
sidérale de la Terre soit T = 23 h 56 min 4 s. Calculons à quelle
altitude il faut le placer en utilisant la relation (7):
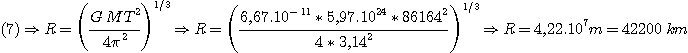
Or h = R -RT ==> h = 42200 - 6400 ==> h =
35 800 km (la Lune est10 fois plus loin et elle tourne en environ 1 mois).
Note 3: Cas des planètes
extra-solaires ou exoplanètes: prenons comme exemple
cette planète étrange découverte en 1999. Elle tourne en 3,5
jours autour
d'une étoile de la constellation de Pégase. Cette étoile et la planète sont
situées à 150 années-lumière du Soleil.
Elle fait partie des 102 planètes extra-solaires connues à ce jour. Sa
particularité est qu'elle est entourée d'une atmosphère
découverte récemment, pas de l'air, mais un
gaz constitué principalement de vapeur de
sodium, métal qui fond à 98 °C.
Cette atmosphère a été découverte grâce à
un phénomène d'éclipse
partielle.
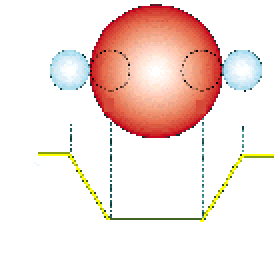
Lors du passage de la planète devant l'étoile,
la brillance de celle-ci chute progressivement jusqu'à un minimum puis augmente progressivement
jusqu'à un maximum:
cela permet de mesurer le diamètre de la planète et de détecter
une éventuelle atmosphère.
Evaluons la distance de cette planète à son étoile en utilisant la
troisième loi de Kepler et en considérant que l'étoile a la même masse que le
Soleil. Pour celà nous disposons du cas de Mercure
(on aurait pu prendre la Terre) qui est à 57 millions de km du Soleil et qui accomplit une
révolution en 88 jours.Le symbole du jour est j ou d (day).
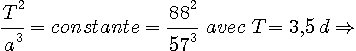
On notera que sous cette forme, on peut utiliser n'importe
quelle unité pourvu qu'elle soit un multiple
ou un sous-multiple d'une unité
internationale.

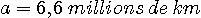
Pour donner un
exemple, le Soleil a un diamètre de 1 400 000 km. La planète est donc toute
proche de la surface de son étoile et sa température est très élevée (environ
1200 °C). Les astronomes espèrent trouver dans l'atmosphère
de cette planète des gaz tels le méthane, composé organique,
mais il, faut savoir que les liaisons chimiques dans ces molécules organiques
sont très fragiles et résistent mal à des températures
élevées.

 SP = R, rayon de l'orbite circulaire est, dans ce cas, le demi grand axe.(On
l'appelle parfois le rayon vecteur).
SP = R, rayon de l'orbite circulaire est, dans ce cas, le demi grand axe.(On
l'appelle parfois le rayon vecteur).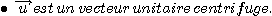

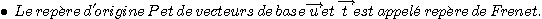
 Nous avons vu les relations suivantes:
Nous avons vu les relations suivantes: